数组中出现次数超过一半的数字

题目描述

数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。
你可以假设数组是非空的，并且给定的数组总是存在多数元素。
示例 1:

输入: [1, 2, 3, 2, 2, 2, 5, 4, 2]
输出: 2

限制：
1 <= 数组长度 <= 50000

题目链接

Leetcode

题目解答

解法一

哈希表统计，遍历数组统计每个元素出现的次数，然后从哈希表中找出 val 最大的 key 就是所需结果。

时间复杂度:$O(n)$ 空间复杂度:$O(n)$

class Solution {
    public int majorityElement(int[] nums) {
        Map<Integer, Integer> map = new HashMap<>();
        for (int num : nums) {
            map.put(num, map.getOrDefault(num, 0) + 1);
        }
        int majority = -1, maxcount = 0;
        for (Integer key : map.keySet()) {
            int val = map.get(key);
            if (val > maxcount) {
                maxcount = val;
                majority = key;
            }
        }
        return majority;
    }
}

简化版

题目要求是找出数组中出现次数超过数组长度一半的数字，我们可以直接在遍历统计过程中判断一个元素出现的次数是否已经超过数组长度的一半，如果是就直接返回当前结果，这样能在一些情况下能够提前返回结果，而不用遍历整个数组，同时也能使代码得到简化。

class Solution {
    public int majorityElement(int[] nums) {
        Map<Integer, Integer> map = new HashMap<>();
        int limit = nums.length >> 1;
        for (int num : nums) {
            int count = map.getOrDefault(num, 0) + 1;
            if (count > limit) return num;
            map.put(num, count);
        }
        return -1;
    }
}

执行用时：13 ms, 在所有 Java 提交中击败了26.95%的用户
内存消耗：43.6 MB, 在所有 Java 提交中击败了31.77%的用户

解法二

数组排序，数组中一个元素出现次数如果超过数组长度的一半，那么在数组有序的情况下，数组中间值一定就是这个元素。

时间复杂度:$O(n\log{}n)$ 空间复杂度:$O(\log{}n)$

class Solution {
    public int majorityElement(int[] nums) {
        Arrays.sort(nums);
        return nums[nums.length / 2];
    }
}

执行用时：2 ms, 在所有 Java 提交中击败了60.67%的用户
内存消耗：44.5 MB, 在所有 Java 提交中击败了5.00%的用户

解法三

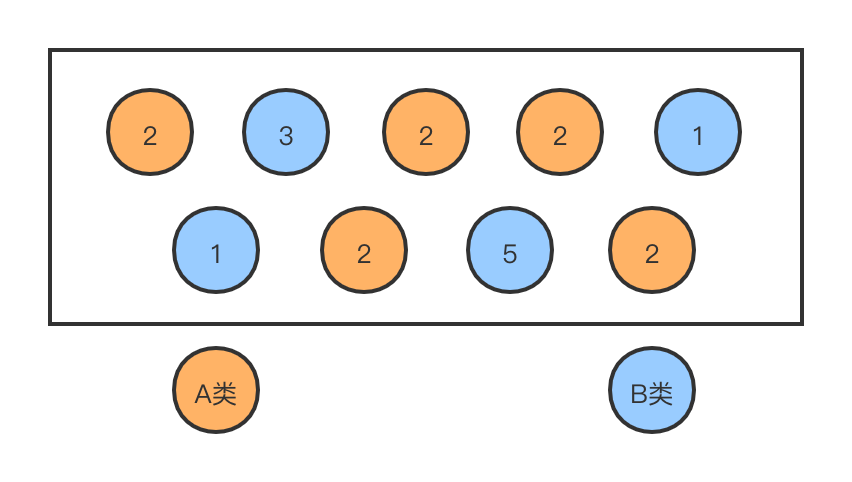
摩尔投票法，核心思想是在一组元素中，如果有元素数量上占优势，也就是超过元素总数的一半，此时所有元素可以被分为两类，我们把数量占优势的元素记为 A，把其他的元素记为 B，对于 A 类元素而言，在所有元素中数量最多，且 A 类中的元素也全部相同，对于 B 类元素而言，在所有元素中数量相对较少，且 B 类中的元素可能相同也可能不同。在这种情况下，我们用一个 A 类元素抵消掉一个 B 类元素，很明显，B 类元素会首先被消耗完，剩下的元素就都是 A 类元素。从算法实现上来说，一开始不知道那个元素是 A 类元素，那个元素是 B 类元素，所以先选定一个候选者 candidate 然后对候选者进行投票，如果当前元素和候选者相同，票数加1，否则票数减1，一个候选者得票为0时，将被下一个候选者替换，最终剩下的候选者就是出现次数最多的元素。

时间复杂度:$O(n)$ 空间复杂度:$O(1)$

class Solution {
    public int majorityElement(int[] nums) {
        int count = 0, candidate = -1;
        for (int num : nums) {
            if (count == 0) {
                candidate = num;
            }
            count += (num == candidate) ? 1 : -1;
        }
        return candidate;
    }
}

执行用时：1 ms, 在所有 Java 提交中击败了99.95%的用户
内存消耗：41.7 MB, 在所有 Java 提交中击败了68.26%的用户